Algorithms From Scratch: K-Nearest Neighbors Classifier

Algos from Scratch: K-Nearest Neighbors

To me, K-Nearest neighbors is the most intutive algorithm for classifcation. If you want to find what group a certain data point belongs to, look at the groups of the point around it and set it to the most common value.

Today, we’ll build a classifier using KNN that determines the species of flower from three options.

Iris Dataset

The Iris dataset is the simple go-to for classification problems. First import numpy, matplotlib, and load_iris. Then, load the dataset into “df”.

import matplotlib.pyplot as plt
import numpy as np

from sklearn.datasets import load_iris

df = load_iris()

First, let’s check out the dataset.

df.keys()

dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename', 'data_module'])

df.target_names

['setosa', 'versicolor', 'virginica']

df.feature_names

['sepal length (cm)',
 'sepal width (cm)',
 'petal length (cm)',
 'petal width (cm)']

So, we’re gonna use the sepal length and width — the stiffer part below the petal — and the petal length and width to determine whether the flower is an iris setosa, versicolor, or virginica.

df.data holds the feature data we want and df.target has the flower type.

figure, axis = plt.subplots(2, 2,figsize=(10,10))
plt.figure(figsize=(6,8))

axis[0,0].scatter(X[:,0],X[:,1])
axis[0,0].set_title("Sepal Length x Sepal Width")
axis[0,0].set_xlabel("Sepal Length")
axis[0,0].set_ylabel("Sepal Width")

axis[0,1].scatter(X[:,2],X[:,3])
axis[0,1].set_title("Petal Length x Petal Width")
axis[0,1].set_xlabel("Petal Length")
axis[0,1].set_ylabel("Petal Width")

axis[1,0].scatter(X[:,0],X[:,2])
axis[1,0].set_title("Sepal Length x Petal Length")
axis[1,0].set_xlabel("Sepal Length")
axis[1,0].set_ylabel("Petal Length")

axis[1,1].scatter(X[:,1],X[:,3])
axis[1,1].set_title("Sepal Width x Petal Width")
axis[1,1].set_xlabel("Sepal Width")
axis[1,1].set_ylabel("Petal Width")

plt.show()

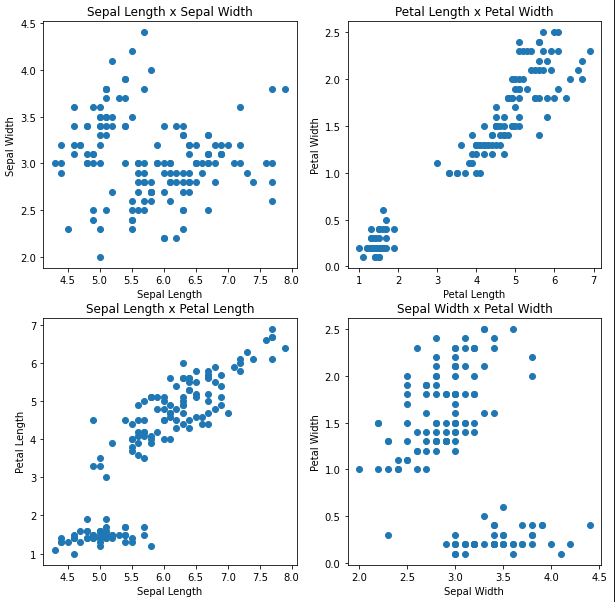
As you can see, some of these plots show two very distinct groups. We have three separate flowers though. Clearly, the data isn’t so obviously separable.

Running a correlation matrix on this data gives some more insight.

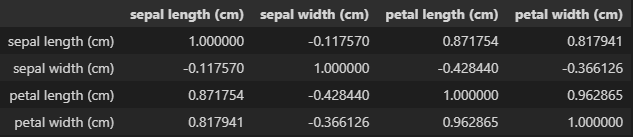
If you read through the documentation on this dataset from sklearns website, you’ll see that “one class is linearly separable from the other 2; the latter are NOT linearly separable from each other.” KNN, however, is not a linear classifier.

KNN

To be more precise about K-nearest neighbors, let’s break it down into steps for one individual data point.

Create empty array to store the distance from our test point to a certain data point and it’s corresponding index
Loop through training set
Calculate distance between our point and the training point
Store that distance and its point in the array from 1
Once done with looping, sort the array by the distances in ascending order
Isolate the k-nearest neighbors
Get the corresponding flower class from the label dataset
Find the most common occuring class and return this

That’s really all there is to making a classifcation.

Code

The first thing I want to do is prepare the dataset. I want to keep some test points to test out our KNN on, so I’m gonna use from sklearn.model_selection import train_test_split with a test size of .2 on df.data and df.target.

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(df.data,df.target,test_size=.2,train_size=.8, random_state=42, shuffle=True)

Now onto the KNN class.

class KNN:
    def __init__(self,x_train, y_train,x_test,y_test, num_neighbors):
        self.x_train = x_train
        self.y_train = y_train
        self.x_test = x_test
        self.y_test = y_test
        self.num_neighbors = num_neighbors

Now to create an individual classifier. Following the steps above, we first create the empty array then loop through the training set. Using enumerate to get both the index and value easily, I take the euclidean distance between our individual point and the training example, then append that to the distance array along with the index.

dist_and_ind = []

for ix,ex in enumerate(self.x_train):
            dist = euclidean_distance(x_test_individual,ex)
            dist_and_ind.append([dist,ix])

By the way, this is the euclidean distance function — it’s very simple.

def euclidean_distance(x1,x2):
    x1=np.array(x1)
    x2=np.array(x2)
    return np.sqrt(np.sum(np.square(x1-x2)))

Now we’ve got all of our distances for that test point. To find the closest point, I used np.argsort just on the distance column of dist_and_ind(). Take the first num_neighbors of the distance array and just keep the indices.

dist_and_ind = np.array(dist_and_ind)
dist_and_ind = dist_and_ind[dist_and_ind[:,0].argsort()]
desired_indices = dist_and_ind[:self.num_neighbors,1].astype(np.int32)

Finally, we can use those indices of the close points to find their corresponding flower class. We want the most common occurence. So rounding the mean value will do.

return np.round(np.mean(self.y_train[desired_indices]))

That looks good! Here’s the full thing.

def classify_individual(self, x_test_individual):
        dist_and_ind = []
        for ix,ex in enumerate(self.x_train):
            dist = euclidean_distance(x_test_individual,ex)
            dist_and_ind.append([dist,ix])
      
        dist_and_ind = np.array(dist_and_ind)
        dist_and_ind = dist_and_ind[dist_and_ind[:,0].argsort()]
        desired_indices = dist_and_ind[:self.num_neighbors,1].astype(np.int32)
        return np.round(np.mean(self.y_train[desired_indices]))

All the rest we have to do is just apply this function to all the test points. I

def classify(self):
        pred_labels=[]
        for i in self.x_test:
            pred_label = self.classify_individual(i)
            pred_labels.append(pred_label)

Here’s the full class:

class KNN:
    def __init__(self,x_train, y_train,x_test,y_test, num_neighbors):
        self.x_train = x_train
        self.y_train = y_train
        self.x_test = x_test
        self.y_test = y_test
        self.num_neighbors = num_neighbors
    def classify_individual(self, x_test_individual):
        dist_and_ind = []
        for ix,ex in enumerate(self.x_train):
            dist = euclidean_distance(x_test_individual,ex)
            dist_and_ind.append([dist,ix])
      
        dist_and_ind = np.array(dist_and_ind)
        dist_and_ind = dist_and_ind[dist_and_ind[:,0].argsort()]
        desired_indices = dist_and_ind[:self.num_neighbors,1].astype(np.int32)
        return np.round(np.mean(self.y_train[desired_indices]))

    def classify(self):
        pred_labels=[]
        for i in self.x_test:
            pred_label = self.classify_individual(i)
            pred_labels.append(pred_label)
        
        return pred_labels
    def error(self):
        pred_labels = self.classify()
        return np.mean( pred_labels != self.y_test )

The last error function is just to determine the percentage of wrong guesses.

The Moment of Truth

Initialize our KNN object.

knn = KNN(X_train,y_train,X_test,y_test,5)

Run the error.

knn.error()

0.0

Success! Out of 15 test points, our KNN classifier didn’t make a single mistake, even with those tricky non-linear groups that seemed difficult to separate.